Repository Summary
| Description | dual quaternions libraries |
| Checkout URI | https://github.com/Achllle/dual_quaternions.git |
| VCS Type | git |
| VCS Version | 0.3.2 |
| Last Updated | 2020-06-12 |
| Dev Status | MAINTAINED |
| CI status | No Continuous Integration |
| Released | RELEASED |
| Tags | No category tags. |
| Contributing |
Help Wanted (0)
Good First Issues (0) Pull Requests to Review (0) |
Packages
| Name | Version |
|---|---|
| dual_quaternions | 0.3.2 |
README
Dual Quaternions
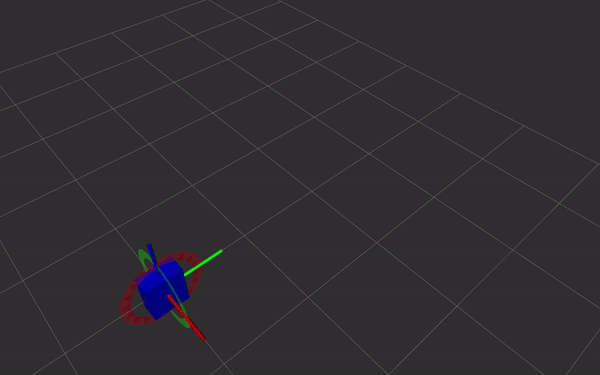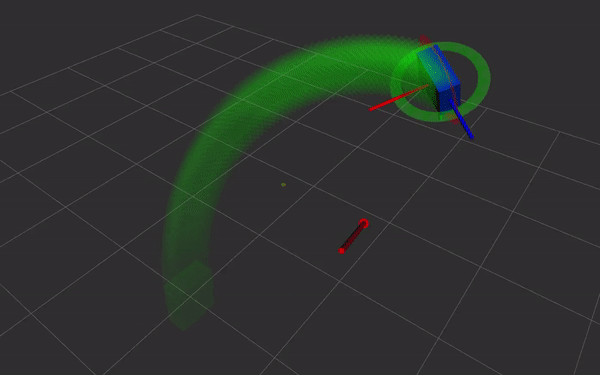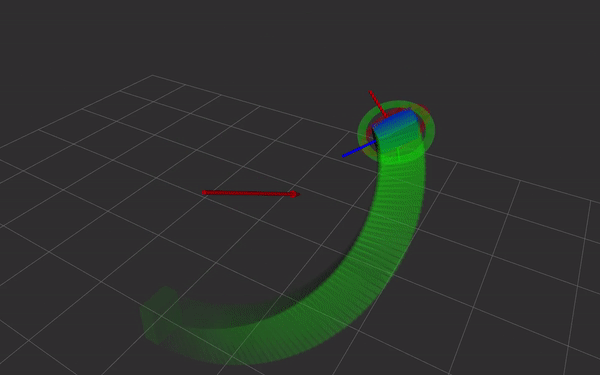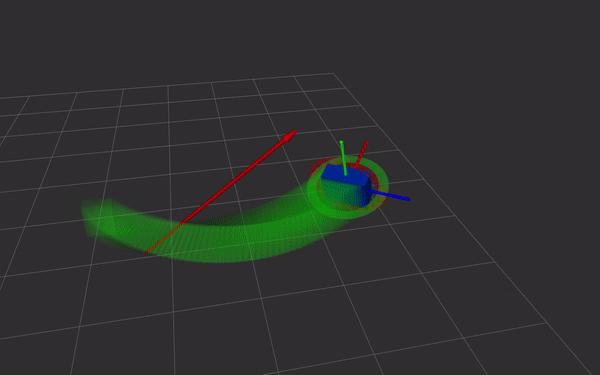
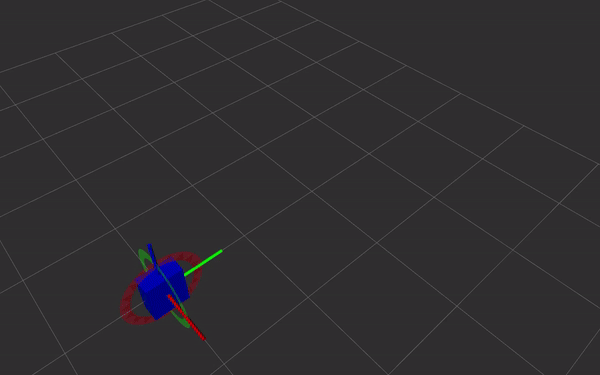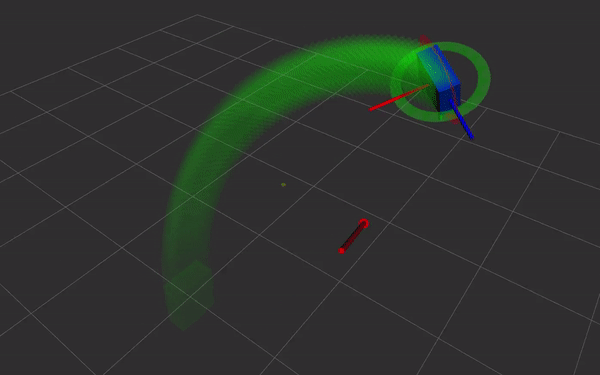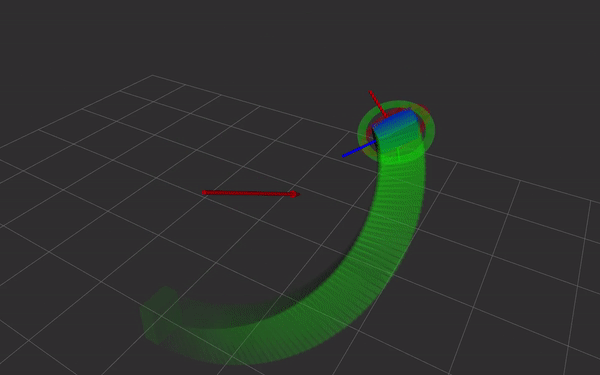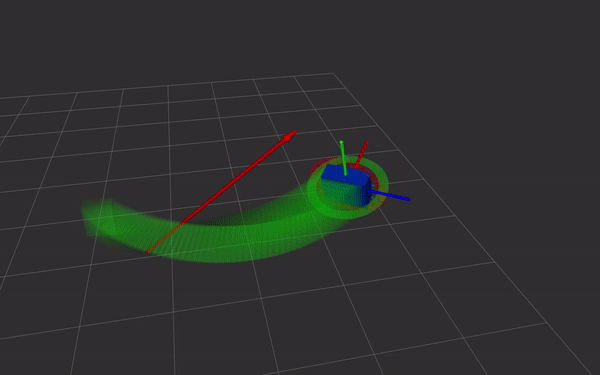
Dual quaternions are a way of representing rigid body transformations,
just like homogeneous transformations do. Instead of using a 4 by 4
matrix, the transformation is represented as two quaternions. This has
several advantages, which are listed under Why use dual
quaternions? The term 'dual' refers to
dual number theory, which allows representing numbers (or in this case
quaternions) very similar to complex numbers with the difference being
that i{.sourceCode} or j{.sourceCode} becomes e{.sourceCode}
(epsilon) and instead of i^2 = -1{.sourceCode} we have
e^2 = 0{.sourceCode}. This allows e.g. multiplication of two dual
quaternions to work in the same way as homogeneous matrix
multiplication.
For more information on dual quaternions, take a look at the References. For conversion from and to common ROS messages, see dual_quaternions_ros.
Why use dual quaternions?
- dual quaternions have all the advantages of quaternions including unambiguous representation, no gimbal lock, compact representation
- direct and simple relation with screw theory. Simple and fast Screw Linear Interpolation (ScLERP) which is shortest path on the manifold
- dual quaternions have an exact tangent / derivative due to dual number theory (higher order taylor series are exactly zero)
- we want to use quaternions but they can only handle rotation. Dual quaternions are the correct extension to handle translations as well.
- easy normalization. Homogeneous tranformation matrices are orthogonal and due to floating point errors operations on them often result in matrices that need to be renormalized. This can be done using the Gram-Schmidt method but that is a slow algorithm. Quaternion normalization is very fast.
- mathematically pleasing
Installation
pip
``` {.sourceCode .bash} pip install dual_quaternions
### ROS package
Release into apt is on its way. Until then you\'ll have to build the
catkin package from source.
``` {.sourceCode .bash}
cd ~/catkin_ws/src
git clone https://github.com/Achllle/dual_quaternions
cd ..
catkin_make
Usage
Import using:
from dual_quaternions import DualQuaternion
References
- K. Daniilidis, E. Bayro-Corrochano, "The dual quaternion approach to hand-eye calibration", IEEE International Conference on Pattern Recognition, 1996
- Kavan, Ladislav & Collins, Steven & Zara, Jiri & O'Sullivan, Carol. (2007). Skinning with dual quaternions. I3D. 39-46. 10.1145/1230100.1230107.
- Kenwright, B. (2012). A Beginners Guide to Dual-Quaternions What They Are, How They Work, and How to Use Them for 3D Character Hierarchies.
- Furrer, Fadri & Fehr, Marius & Novkovic, Tonci & Sommer, Hannes & Gilitschenski, Igor & Siegwart, Roland. (2018). Evaluation of Combined Time-Offset Estimation and Hand-Eye Calibration on Robotic Datasets. 145-159. 10.1007/978-3-319-67361-5_10.
CONTRIBUTING
Repository Summary
| Description | dual quaternions libraries |
| Checkout URI | https://github.com/Achllle/dual_quaternions.git |
| VCS Type | git |
| VCS Version | master |
| Last Updated | 2024-10-22 |
| Dev Status | MAINTAINED |
| CI status | No Continuous Integration |
| Released | RELEASED |
| Tags | No category tags. |
| Contributing |
Help Wanted (0)
Good First Issues (0) Pull Requests to Review (0) |
Packages
| Name | Version |
|---|---|
| dual_quaternions | 0.3.2 |
README
Dual Quaternions
Dual quaternions are a way of representing rigid body transformations, just like homogeneous transformations do. Instead of using a 4x4 matrix, the transformation is represented as two quaternions. This has several advantages, which are listed under Why use dual quaternions?. The term ‘dual’ refers to dual number theory, which allows representing numbers (or in this case quaternions) very similar to complex numbers, with the difference being that i or j becomes e (epsilon), and instead of i^2 = -1, we have e^2 = 0. This allows, for example, the multiplication of two dual quaternions to work in the same way as homogeneous matrix multiplication.
For more information on dual quaternions, take a look at the References. For conversion from and to common ROS messages, see dual_quaternions_ros.
Why use dual quaternions?
- dual quaternions have all the advantages of quaternions including unambiguous representation, no gimbal lock, compact representation
- direct and simple relation with screw theory. Simple and fast Screw Linear Interpolation (ScLERP) which is shortest path on the manifold
- dual quaternions have an exact tangent / derivative due to dual number theory (higher order taylor series are exactly zero)
- we want to use quaternions but they can only handle rotation. Dual quaternions are the correct extension to handle translations as well.
- easy normalization. Homogeneous tranformation matrices are orthogonal and due to floating point errors operations on them often result in matrices that need to be renormalized. This can be done using the Gram-Schmidt method but that is a slow algorithm. Quaternion normalization is very fast.
- mathematically pleasing
Installation
pip install dual_quaternions
Usage
from dual_quaternions import DualQuaternion
References
- \K. Daniilidis, E. Bayro-Corrochano, “The dual quaternion approach to hand-eye calibration”, IEEE International Conference on Pattern Recognition, 1996
- Kavan, Ladislav & Collins, Steven & Zara, Jiri & O’Sullivan, Carol. (2007). Skinning with dual quaternions. I3D. 39-46. 10.1145/1230100.1230107.
- Kenwright, B. (2012). A Beginners Guide to Dual-Quaternions What They Are, How They Work, and How to Use Them for 3D Character Hierarchies.
- Furrer, Fadri & Fehr, Marius & Novkovic, Tonci & Sommer, Hannes & Gilitschenski, Igor & Siegwart, Roland. (2018). Evaluation of Combined Time-Offset Estimation and Hand-Eye Calibration on Robotic Datasets. 145-159. 10.1007/978-3-319-67361-5_10.
CONTRIBUTING
Repository Summary
| Description | dual quaternions libraries |
| Checkout URI | https://github.com/Achllle/dual_quaternions.git |
| VCS Type | git |
| VCS Version | 0.3.2 |
| Last Updated | 2020-06-12 |
| Dev Status | MAINTAINED |
| CI status | No Continuous Integration |
| Released | RELEASED |
| Tags | No category tags. |
| Contributing |
Help Wanted (0)
Good First Issues (0) Pull Requests to Review (0) |
Packages
| Name | Version |
|---|---|
| dual_quaternions | 0.3.2 |
README
Dual Quaternions
Dual quaternions are a way of representing rigid body transformations,
just like homogeneous transformations do. Instead of using a 4 by 4
matrix, the transformation is represented as two quaternions. This has
several advantages, which are listed under Why use dual
quaternions? The term 'dual' refers to
dual number theory, which allows representing numbers (or in this case
quaternions) very similar to complex numbers with the difference being
that i{.sourceCode} or j{.sourceCode} becomes e{.sourceCode}
(epsilon) and instead of i^2 = -1{.sourceCode} we have
e^2 = 0{.sourceCode}. This allows e.g. multiplication of two dual
quaternions to work in the same way as homogeneous matrix
multiplication.
For more information on dual quaternions, take a look at the References. For conversion from and to common ROS messages, see dual_quaternions_ros.
Why use dual quaternions?
- dual quaternions have all the advantages of quaternions including unambiguous representation, no gimbal lock, compact representation
- direct and simple relation with screw theory. Simple and fast Screw Linear Interpolation (ScLERP) which is shortest path on the manifold
- dual quaternions have an exact tangent / derivative due to dual number theory (higher order taylor series are exactly zero)
- we want to use quaternions but they can only handle rotation. Dual quaternions are the correct extension to handle translations as well.
- easy normalization. Homogeneous tranformation matrices are orthogonal and due to floating point errors operations on them often result in matrices that need to be renormalized. This can be done using the Gram-Schmidt method but that is a slow algorithm. Quaternion normalization is very fast.
- mathematically pleasing
Installation
pip
``` {.sourceCode .bash} pip install dual_quaternions
### ROS package
Release into apt is on its way. Until then you\'ll have to build the
catkin package from source.
``` {.sourceCode .bash}
cd ~/catkin_ws/src
git clone https://github.com/Achllle/dual_quaternions
cd ..
catkin_make
Usage
Import using:
from dual_quaternions import DualQuaternion
References
- K. Daniilidis, E. Bayro-Corrochano, "The dual quaternion approach to hand-eye calibration", IEEE International Conference on Pattern Recognition, 1996
- Kavan, Ladislav & Collins, Steven & Zara, Jiri & O'Sullivan, Carol. (2007). Skinning with dual quaternions. I3D. 39-46. 10.1145/1230100.1230107.
- Kenwright, B. (2012). A Beginners Guide to Dual-Quaternions What They Are, How They Work, and How to Use Them for 3D Character Hierarchies.
- Furrer, Fadri & Fehr, Marius & Novkovic, Tonci & Sommer, Hannes & Gilitschenski, Igor & Siegwart, Roland. (2018). Evaluation of Combined Time-Offset Estimation and Hand-Eye Calibration on Robotic Datasets. 145-159. 10.1007/978-3-319-67361-5_10.


 {.align-center}
{.align-center}